摘 要:本研究主要探究思维模式、数学学业成绩、问题提出能力之间的关系。以乌鲁木齐市333名小学五年级学生为研究对象,使用问卷和测试卷等研究工具考察学生的思维模式、数学学业成绩以及学生在三种问题提出情境(无结构情境、半结构情境、结构情境)中的问题提出表现。本研究从问题提出的数量与质量两个层面对学生所提出的问题进行编码分析,数量方面包括学生所提出的数学问题的原始数量、有效数量、异质数量和流畅数量,质量方面包括学生所提出的数学问题的灵活性和创新性两个方面。研究发现,思维模式高分组与低分组学生在问题提出能力上存在显著性差异;数学学业成绩与问题提出能力的相关关系只存在于思维模式低分组,并不存在于思维模式高分组;不同情境下,思维模式、数学学业成绩和问题提出能力的关系不尽相同。本研究针在学生思维模式、学业成绩与问题提出能力的关系方面进行了初步探索,研究工具和研究结果对进一步分析少数民族地区学生的思维模式和问题提出能力提供了重要借鉴。
关键词:民族地区;数学教育;思维模式;成长型思维;学业成绩;问题提出
一、问题的提出
民族地区基础教育阶段数学教育已经取得了长足的进步,例如,完善民族地区数学教科书建设,健全数学师资培养体系等。[1]但是,目前民族地区数学学习效果仍有较大的进步空间。当前研究普遍关注少数民族地区学生对基本数学知识的掌握水平,关于少数民族学生高阶数学思维发展的研究相对较少。
问题提出和问题解决能力已成为21世纪人才培养的焦点,也是基础教育研究的热点。[2][3][4][5][6]汪秉彝和吕传汉提出,通过建立“设置数学情境—提出数学问题—解决数学问题—联系实际应用”的数学教育模式,培养学生的创造性。[7]聂必凯等认为问题提出活动不仅能够提高学生问题解决能力,而且能够有效改进学生对数学的态度。[8]夏小刚认为问题提出能力是一种综合性较强的数学能力,因此问题提出能力的评价需要确保可操作性和科学性。[9]蔡金法(Cai.J)等认为,研究者不仅要探讨数学问题提出的理念和评价,也要帮助教师将问题提出应用于实际课堂教学中。[10]
以往研究指出,小学生的“问题解决”与“问题提出”能力之间具有很强的正相关性。陈丽敏等发现,我国四年级小学生的问题提出能力与问题解决能力之间存在显著相关性。[11]尼瑞达·F.埃勒顿(Nerida F.Ellerton)等对11-13岁学生的研究发现,问题解决能力较强的学生提出的问题更复杂。[12]爱德华·A.西尔弗(Edward A. Silver)等发现,在问题解决方面表现较好的小学生,能够提出更多、更复杂的问题。[13]范德沃勒·J.A(Van De Walle・J.A)等学者发现,在数学问题解决上存在障碍的小学生,在问题提出上也会出现困难。[14]但是,问题解决与问题提出也存在明显的不同。汪秉彝和吕传汉发现,小学生数学问题解决的表现优于数学问题提出的表现。[15]先伟·Y.范哈本(Xianwei Y.Van Harpen)等指出,问题提出是一项创造性活动,问题提出能力代表了学生创造性的一个维度。[16]在问题解决过程中的创新能力,主要体现在使用不同的解题策略层面。[17]俞国良等学者建议使用问题提出能力来考察小学生的创新能力。[18]
成长型思维模式理论的提出源自心理学教授卡罗尔·S.德韦克(Carol S.Dweck)对内隐认知理论的研究。德韦克发现,学生思维模式对其学业与长远发展有重大影响,因此她提出应当从思维模式视角审视学校教育,通过培养学生的成长型思维模式来促进学生的学业发展。[19][20][21]借鉴德韦克等人的研究,彭凯平团队发现:成长型思维模式的培养不仅可以培养学生的积极心态,还可以提高学生的学业成绩。[22]此外,彭凯平团队还对三年级到九年级学生进行取样调查,发现拥有成长型思维模式的学生具有更强的毅力。[23]2018年国际学生评估项目(Programme for International Student Assessment, PISA)测试结果显示,成长型思维模式倾向越强,学生的阅读得分越高、自我效能感越强,并且能够以更加积极的心态看待学习。[24]虽然思维模式越来越多地受到研究者的关注和重视,[25]但是对于少数民族地区学生的思维模式的研究几乎没有。
已有研究探讨了成长型思维模式与问题解决能力、问题提出能力的关系。苏·詹妮弗(Suh Jennifer)等学者指出,成长型思维倾向较高的学生在问题解决过程中思考的时间更长、思考问题角度更多元,因此拥有成长型思维倾向的学生表现出更好的毅力和灵活性。[26]乔·博勒(Jo Bodaler)等学者基于对课堂的观察发现,成长型思维倾向高的学生更敢于提出自己的数学问题。[27]此外,先伟·Y.范哈本等学者指出,问题提出能力与数学学业成绩之间具有显著正相关关系。[28]同时,问题提出情境会对学生问题提出的表现产生影响。结构情境在一定程度上引导学生关注情境中的数学概念与关系,进而能够提升学生的问题提出表现。[29]
综上所述,已有研究指出:第一,思维模式会影响小学生的问题解决能力,但是少数民族地区小学生的思维模式的相关研究较少;第二,问题解决和问题提出之间存在较为密切的关系;第三,思维模式与问题提出之间存在潜在的联系;第四,问题提出能力还与数学学业成绩、问题提出情境等因素有关系。这些研究进展启发我们进一步思考,在少数民族地区,思维模式究竟会如何影响小学生的问题提出能力?这些影响在不同问题提出情境下是否会有所不同?另外,思维模式不同的小学生,其数学学业成绩与问题提出能力之间的关系是否会有所不同?
在已有研究基础之上,本研究主要探究思维模式、数学学业成绩、问题提出能力之间的关系。本研究以少数民族地区小学生为研究对象,旨在解决以下研究问题:(1)思维模式不同的小学生在问题提出能力上是否会有所不同?(2)思维模式不同的小学生,其数学学业成绩与问题提出能力的关系上是否会存在不同?(3)在不同的问题提出情境下,上述两个问题是否呈现不同的结果?
二、研究方法
(一)研究对象
笔者长期关注新疆维吾尔自治区小学生数学教育质量发展情况,同时多次参与新疆基础教育质量监测工作。新疆维吾尔自治区具有鲜明的民族文化和地域特色,同时也是教育扶贫的重点区域,针对该地区的教育研究能够为教育扶贫提供针对性建议。因此,本研究聚焦新疆维吾尔自治区小学生,希望能够揭示新疆维吾尔自治区小学生思维模式、数学学业成绩、问题提出能力之间的关系。
在新疆维吾尔自治区收集课堂录像、教师访谈、学生问卷等数据。数据涉及乌鲁木齐市教学质量中等程度的两所小学五年级8个班共计466名学生,本研究从中选择6个班共计333名五年级小学生进行数据分析。研究对象中,男生165人(49.5%),女生168人(50.5%),包括汉族266人(79.9%),维吾尔族19人(57%),哈萨克族5人(15%),回族31人(93%),其他民族12人(36%)。
(二)研究工具
1.思维模式量表
采用德韦克的思维模式量表[30][31],该量表共2个项目。邢淑芬等学者的研究指出,该量表中有两个项目译为汉语后属同义反复。[32]因此本研究借鉴邢淑芬等学者的做法,采用2个项目考察思维模式:(1)我的聪明程度是固定的,很难做出改变;(2)虽然我可以学习新事物,但是我的聪明程度是无法改变的。选项采用6点Likert计分方式,从1分(非常不同意)到6分(非常同意)。本研究中,思维模式量表内部一致性信度(Cronbach’s α)为0.808。
2.数学学业测试
使用《乌鲁木齐市2018-2019学年第一学期质量监测小学五年级数学测试》成绩作为学生数学学业测试成绩。该测试为全市所有小学五年级统考。测试内容主要为人民教育出版社小学数学五年级上册所包含的基础知识。
3.问题提出能力测试
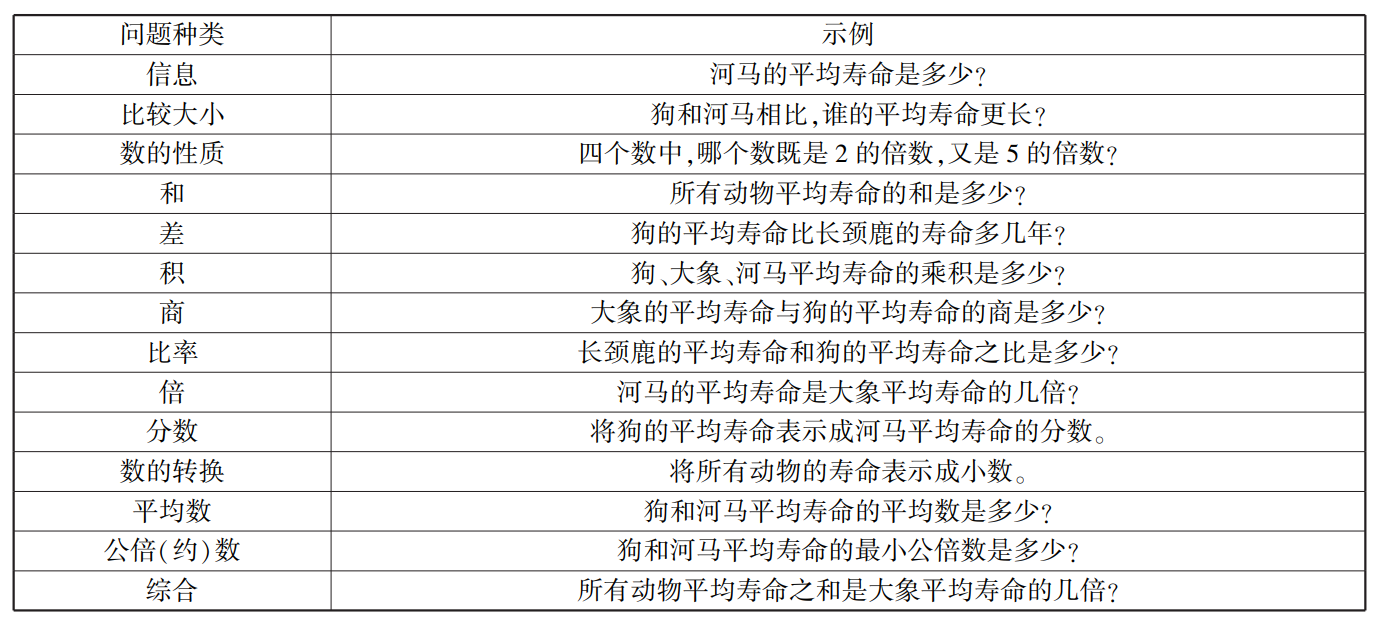
问题提出能力测试主要分为三种情境:无结构情境、半结构情境和结构情境。[33][34]无结构情境包含简单罗列的信息;半结构情境中包含的信息之间具有一定的结构关系;结构情境中,不仅包含情境信息,还包含四个数学问题。本研究中,无结构情境和半结构情境改编自人民教育出版社小学数学四年级上册和五年级上册教科书。[35][36]结构情境改编自蔡金法等人的研究。[37]每个情境都要求学生提出6个数学问题,2个学生认为容易一些的问题,2个难一些的问题和2个很难的问题。三种问题情境如下所示。
(1)无结构情境:下面是几种动物的平均寿命(见表1)。
(2)半结构情境:有一块梯形菜地,种了三种蔬菜(见图1)。
(3)结构情境:观察下面三幅图(见图2)
(a)请画出第四幅图。
(b)第六幅图中有几个黑点?
(c)第六幅图中有几个白点?
(d)第一幅图中有8个白点,第三幅图中有16个白点。请问第几幅图中有44个白点?
表1 四种动物的平均寿命

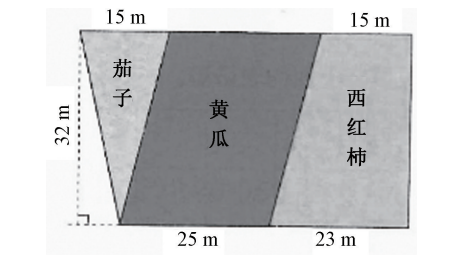
图1 三种情境下问题提出数量的结果分析

图2 三种情境下问题提出数量的结果分析
(三)数据分析过程
1.思维模式的分类标准
截至目前,已有研究中的考察思维模式的量表均来自德韦克及其团队,但是对思维模式的分类标准并不统一,主要存在三种方式:(1)两分法,即按照思维模式得分,分为固定型思维模式和成长型思维模式;(2)三分法,即按照思维模式得分,分为固定型思维模式、混合型思维模式和成长型思维模式;(3)程度法,即不区分成长型与固定型,按照思维模式得分进行成长型思维倾向的程度描述,思维模式得分越高代表成长型思维倾向程度越高,思维模式得分越低代表成长型思维倾向程度越低。第一种方式的代表主要是德韦克及其团队的早期研究,第二种方式的代表是德韦克及其团队的近期研究,第三种方式的代表是PISA2018测试。[38][39][40]近年来,德韦克本人也指出,没有纯粹的成长型思维或者固定型思维,而人们思维模式的差异主要是因为成长型思维的比例不同。[41]
因此,本研究在对思维模式进行分类时,主要采用上面的第三种方式。思维模式量表中2个项目得分(反向题进行反向计分)取平均值作为学生思维模式得分,得分越高表明学生成长型思维倾向越强。
2.问题提出能力的编码框架
综合前人已有研究对问题提出能力的分析框架,本研究从问题提出的数量与质量两个层面对学生所提出的问题进行编码分析。[42][43]
(1)问题提出的数量。考查学生所提出的数学问题的原始数量、有效数量、异质数量和流畅数量,四种数量的最大值均为6,最小值均为0。
第一,原始数量是指学生在测试卷上写出的所有问题的数量,不考虑学生所写出的问题是否与情境契合以及问题表述是否清楚等因素。问题提出的原始数量反映学生在面对问题提出任务时是否能够尝试作答。
第二,有效数量考查学生所写问题的有效性。如果学生提出的问题存在以下情况,将被视为无效问题:问题表述不清,无法理解,或者书写过于潦草,无法辨认;问题与数学知识无关,例如,“大象和狗是否住在动物园中”?;问题与情境信息无关,例如,“狗的速度比大象快多少”?;重复的问题。将无效问题剔除后,得到问题提出的有效数量。
第三,对于满足有效性的数学问题,进一步考查问题提出的异质性,即考查学生所提出的数学问题在结构上是否相同。例如,“河马的平均寿命是狗的平均寿命的几倍”与“狗的平均寿命是河马的平均寿命的几倍”记作结构相同的问题。结构相同的问题仅计数1次。因此,问题提出的异质数量反映学生提出的问题中,包含几种不同的问题结构。
第四,对于结构不同的数学问题,进一步考察问题的流畅性,即问题是否能够根据情境中的信息进行解答,进而得到问题的流畅数量。例如,“西红柿的体积是多少”属于不能够根据情境信息解决的问题,在计算流畅数量时将被剔除。
(2)问题提出的质量。对于满足有效、异质、流畅的数学问题,进一步分析问题提出的质量。问题提出的质量主要包括问题提出的灵活性和创新性两个方面。
灵活性是指学生所提出的问题种类的丰富程度。首先需要对所有学生提出的满足有效、异质、流畅要求的数学问题进行分类(无结构情境的问题分类结果如表2所示)。其次考察每一名学生提出的流畅性数学问题中包含的问题种类,并进行计分。例如,如果一个学生提出6个数学问题,这些问题最终流畅数量为4,而4个问题中包含3个问题种类,则将该同学灵活性得分记为3。每个情境下,学生在问题提出的灵活性得分最大值为6,最小值为0。
表2无结构情境下学生提出的数学问题分类结果
创新性是指学生所提出的问题的独特程度,分为高中低三个层次。对于学生提出的满足有效、异质、流畅要求的问题,逐个考察提出该问题的学生人数和所占比例,问题创新性进行编码和计分如表3所示。例如,在无结构情境下,如果一个学生提出问题流畅数量为6,同时每个问题都属于高创新性层次,则该学生的创新性得分为18。在每个情境下,问题提出创新性得分最大值为18,最小值为0。
表3问题提出创新性的判断与计分

编码过程中发现,一些问题是因为过于简单而导致提出该问题的学生比例低于10%,则这种问题直接被编码为低独特性。例如,无结构情境中,“狗的平均寿命是多少”由于情境中已经给出了狗的平均寿命,因此,虽然提出该问题的学生比例低于10%,仍然被编码为低独特性问题。
2.编码一致性检验
为确保编码分析过程的质量,由两位研究者首先按照编码框架对100名学生提出的问题进行独立编码,对编码不一致的部分进行集体讨论,最终保证编码结果一致性达到100%。在此基础上,其余233名学生提出问题的编码由所有研究者分工完成。
三、结果与分析
(一)学生思维模式和数学学业成绩的整体情况
学生思维模式得分平均值为4.67,标准差为1.31。其中,男生思维模式得分平均值为4.89,标准差为1.20,女生思维模式得分平均值为4.45,标准差为1.38。男生的思维模式得分高于女生(t=3.122,p<0.01),表明男生整体的成长型思维倾向强于女生。
按照思维模式得分进行高低分组。选择成长型思维得分上前27%与后27%的学生,分别标定为成长型思维倾向高分组(简记为GM高分组)和成长型思维倾向低分组(简记为GM低分组)。GM高分组与GM低分组在思维模式得分上存在显著性差异(t= -29.451,p<0.001)。GM高分组的思维模式得分平均值为5.84,标准差为0.23。GM低分组的思维模式得分平均值为2.94,标准差为0.96。
学生数学学业成绩的平均值为89.54,标准差为17.09。其中,男生数学学业成绩平均值为94.13,标准差为9.45,女生数学学业成绩平均值为90.78,标准差为11.39。男生的数学学业成绩高于女生(t=2.915,p<0.01),表明男生整体的数学学业成绩优于女生。
(二)学生问题提出能力的整体情况
1.问题提出的数量
每种情境下的问题提出数量如图3所示。可以发现,三种情境下,问题提出的原始数量和有效数量的平均值都接近于最大值6。而问题提出的异质数量和流畅数量明显下降。三种情境中,结构情境下问题提出的异质数量和流畅数量最高。半结构情境下的问题提出异质数量与流畅数量最低。
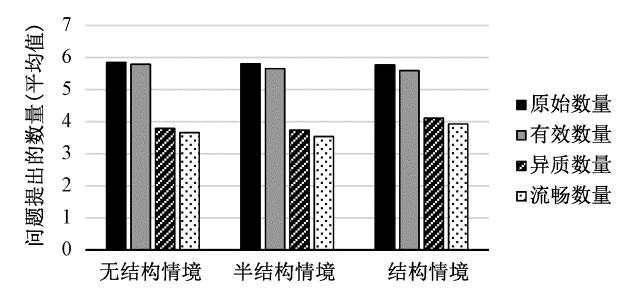
图3三种情境下问题提出数量的结果分析
2.问题提出的质量
每种情境下的问题提出质量如图4所示。无结构情境和结构情境下问题提出的灵活得分相近,而半结构情境下的问题提出的灵活得分最低。结构情境下问题提出的创新得分最高。无结构情境和半结构情境下问题提出的创新得分相近。
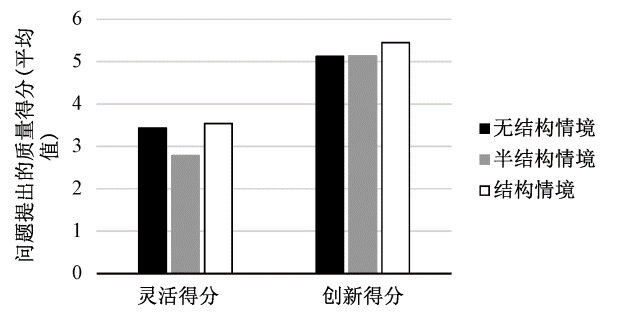
图4三种情境下问题提出质量的结果分析
(三)思维模式、数学学业成绩与问题提出能力之间的相关分析
1.GM高分组与GM低分组学生在数学学业成绩上的差异分析
GM高分组与低分组在数学学业成绩上存在显著性差异(t= -2.828,p<0.01)。GM高分组的数学学业成绩(M=94.25,SD=7.61)显著高于GM低分组的数学学业成绩(M=89.91,SD=13.55)。
2.GM高分组与GM低分组学生在问题提出能力上的差异分析
GM高分组在半结构情境下问题提出的异质得分(t= -2.421,p<0.05)、流畅得分(t= -3.214,p<0.01)、灵活得分(t= -2.753,p<0.01)和结构情境下创新得分(t= -2.270,p<0.03)、灵活得分(t= -2.691,p<0.01)显著高于GM低分组(见表4)。但是,GM高分组与GM低分组在无结构情境下问题提出能力上没有显著性差异。
表4成长型思维倾向高分组与低分组学生问题提出能力的差异分析

3.GM高分组与GM低分组中数学学业成绩与问题提出能力上的相关性
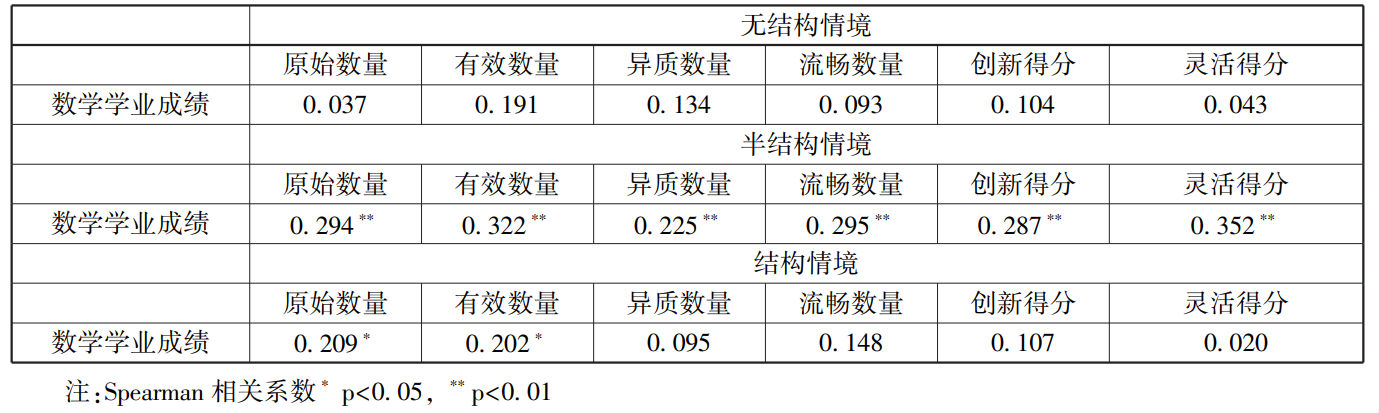
GM高分组学生数学成绩与三种情境下的问题提出得分上,均没有显著相关关系。GM低分组学生数学成绩与半结构情境下问题提出表现全部具有显著相关关系,同时与结构情境下问题提出的原始数量和有效数量具有显著相关关系(见表5)。这说明,GM低分组学生数学学业成绩越好,问题提出得分相对就好。但是,GM高分组学生中并没有出现这种情况。其原因可能在于,GM高分组学生能够更加积极地应对数学问题提出任务,不易受到平时数学学业成绩的影响。
表5成长型思维倾向低分组学生数学学业表现与问题提出能力的相关分析
四、结论与展望
(一)研究结论
1.思维模式高分组与低分组学生在问题提出能力上存在显著差异
本研究发现,思维模式高分组在半结构和结构情境下的问题提出能力显著优于思维模式低分组。具体而言,思维模式高分组在半结构情境下问题提出的流畅得分和灵活得分显著高于思维模式低分组,同时在结构情境下问题提出的创新得分和灵活得分也显著高于思维模式低分组。
苏·詹妮弗等学者指出,成长型思维倾向高的学生在问题解决中表现出更好的毅力和灵活性。[44]本研究发现,成长型思维倾向高的学生在半结构情境下提出的数学问题流畅性和灵活性更好,在结构情境下提出的数学问题创新性和灵活性更好。因此,本研究结果作为实证数据,进一步表明思维模式不仅会影响学生的问题解决能力,也会影响学生的问题提出能力。
2.数学学业成绩与问题提出能力的相关关系只存在于思维模式低分组,并不存在于思维模式高分组
本研究发现,数学学业成绩与问题提出能力的相关关系只存在于思维模式低分组,并不存在于思维模式高分组。先伟·Y.范哈本等学者发现,数学学业成绩与问题提出能力存在显著相关性。[45]本研究则进一步指出,数学基础知识只能预测思维模式低分组学生问题提出能力,并不能预测思维模式高分组的问题提出能力。这表明,在考察问题提出能力与数学学业成绩的关系时,需要将思维模式高分组与低分组学生进行区分。
此外,问题提出与学生平时学习中的数学问题有所不同,在某种程度上对学生造成一定的学习挑战。本研究表明,学生数学学业成绩作为评价结果会影响思维模式不同的学生在面对学习挑战时的表现。这与已有研究的发现是一致的。德戈·杰西卡.L(Degol Jessica L)等学者指出,成长型思维倾向不同的学生,在面对有挑战性的学习任务时会出现不同的表现。[46]成长型思维倾向较低的学生,往往会对自己的能力产生怀疑,从而影响他们的动机和表现,更倾向于选择放弃或者消极拖延。[47][48]而成长型思维倾向较高的学生则表现出更高的学习动机和兴趣,并采取更加积极的策略应对挑战。[49][50]
本研究中,思维模式低分组学生更倾向于认为,“平时数学成绩不理想”等同于“数学能力不足或者不适合学习数学”,因而会影响自己面对“提出数学问题”这一挑战时的心态和表现。数学学业成绩与问题提出能力的相关关系只存在于思维模式低分组,说明成长型思维倾向低的学生在面对学习挑战时,易受到平时学业成绩的影响。
3.不同情境下,思维模式、数学学业成绩和问题提出能力的关系不尽相同
本研究考察了三种不同情境下的问题提出能力。在半结构和结构情境下,思维模式高分组与低分组学生在问题提出能力上存在显著差异。同时,思维模式低分组学生的数学学业成绩与问题提出能力的相关关系只出现在半结构和结构情境下。这表明,思维模式、数学学业成绩和问题提出能力的关系只存在于半结构和结构情境下。这体现了问题提出情境对问题提出能力所产生的影响。
已有研究指出,问题提出的情境会对学生问题提出的表现产生影响。[51]本研究结果印证了已有的研究发现,并且进一步表明,问题提出的情境设置不仅影响学生的问题提出表现,而且可能会进一步影响思维模式、数学学业成绩和问题提出能力的关系。同时,这也反映出思维模式对问题提出能力的影响与情境设置有关。
(二)研究展望
提出数学问题的过程中,学生不仅需要数学思考与推理,同时也需要使用语言将数学问题进行表述[52],因此学生语文成绩可能会对学生问题提出的表现造成一定影响。本研究没有收集研究对象的语文成绩,因此无法揭示语文成绩与学生思维模式和问题提出能力的关系。今后研究可以同时收集学生的语文和数学两个学科的学业表现,综合研究学生的语言水平、数学能力和思维模式对问题提出的影响。
以往研究指出,思维模式会随着学生的年龄而发生变化[53],但是本研究只考察了一个年级,无法考查学生思维模式的发展情况及其对问题提出能力的影响。今后研究可以同时收集多个年级学生的思维模式水平,或者进行较长时间的跟踪研究,综合考虑学生思维模式的发展以及学生问题提出能力的动态变化,进而探究思维模式发展对问题提出能力影响的一般规律。
本研究选取乌鲁木齐市城区的学生样本,在学生思维模式、学业成绩与问题提出能力的关系方面进行了初步探索,研究工具和研究结果对进一步分析少数民族地区学生的思维模式、问题提出能力提供了一定的借鉴与参考。今后研究可以考虑选取更具代表性的少数民族学生样本,更为全面地考察民族地区学生思维模式与问题提出能力。
参考文献:
[1]王建磐.中国数学教育:传统与现实[M].南京:江苏教育出版社,2009.
[2][7][15]汪秉彝,吕传汉.创新与中小学数学教育[J].数学教育学报,2000,9(4).
[3][8]聂必凯,汪秉彝,吕传汉.关于数学问题提出的若干思考[J].数学教育学报,2003,12(2).
[4][11]陈丽敏,VERSCHAFFEL L,李雪梅.问题提出和问题解决之间关系的问卷调查「J].数学教育学报,2004,13(4).
[5][9]夏小刚.国内外数学问题提出教学研究的回顾与反思[J].数学教育学报,2005,14(3).
[6][10]蔡金法,姚一玲.数学“问题提出”教学的理论基础和实践研究[J].数学教育学报,2019,28(4).
[12]ELLERTON N F. Children's made-up mathematics problems-a new perspective on talented mathematicians[J]. Educational studies in mathematics,1986,17(3):261-271.
[13]SILVER E A. On mathematical problem posing[J]. For the learning of mathematics,1994,14(1):19-28.
[14]VAN DE WALLE J A. Elementary and middle school mathematics[M]. Boston: Pearson Education Inc,2013:14-15.
[16][28][33][42][45]VAN HARPEN X Y, PRESMEG N C. An investigation of relationships between students' mathematical problem-posing abilities and their mathematical content knowledge[J]. Educational studies in mathematics,2013,83(1):117-132.
[17]ARIKAN EE, UNAL H. Investigation of problem-solving and problem-posing abilities of seventh-grade students[J]. Educational sciences: theory and practice,2015,15(5):1403-1416.
[18]俞国良,侯瑞鹤.问题提出、认知风格与学校教育中的创造力培养[J].教育科学,2004,20(4).
[19]MANGELS J A, BUTTERFIELD B, LAMB J, et al. Why do beliefs about intelligence influence learning success? A social cognitive neuroscience model[J]. Social cognitive and affective neuroscience,2006,1(2):75-86
[20]HAIMOVITZ K, DWECK C S. What predicts children's fixed and growth intelligence mind-sets? Not their parents views of intelligence but their parents' views of failure[J]. Psychological science,2016,27(6):859-869.
[21]李抗,杨文登.从归因疗法到内隐理念:德韦克的心理学理论体系及影响[J].心理科学进展,2015,23(4).
[22]ZENG G, HOU H,PENG K. Effect of growth mindset on school engagement and psychological well-being of Chinese primary and middle school students:the mediating role of resilience[J]. Frontiers in psychology,2016(7):1-8
[23]ZHAO Y, NIU G,HOU H, et al. From growth mindset to grit in Chinese schools:the mediating roles of learning motivations[J]. Frontiers in psychology,2018(9):1-7.
[24][40]SCHLEICHER A. PISA 2018:insights and interpretations[EB/OL].https://www.oecd.org/pisa/PISA%202018%20Insights%20and%20Interpretations%20FINAL%20PDF.pdf
[25]CAI J, MORRIS A, HWANG S, et al. Improving the impact of educational research[J]. Journal for research in mathematics education,2017,48(1):2-6.
[26][44]SUH J, GRAHAM S, FERRANONE T, et al. Developing persistent and flexible problem solvers with a growth mindset [M]//BRAHIER D J. Motivation and disposition pathways to learning mathematics. New York: National council of teachers of mathematics,2011:169-184.
[27]BOALER J. Mathematical mindsets: unleashing students' potential through creative math, inspiring messages and innovative teaching[M]. Chappaqua: John Wiley Sons,2015:141-143.
[29][51]CHRISTOU C, MOUSOULIDES N, PITTALIS M, et al. An empirical taxonomy of problem posing processes[J].ZDM mathematics education,2005,37(3):149-158.
[30]DWECK C S.Self-theories:their role in motivation, personality,and development[M].Philadelphia: Psychology press,1999:29-31.
[31]DWECK C S, CHIU C,HONG Y. Implicit theories and their role in judgments and reactions: a word from two perspectives[J]. Psychological inquiry,1995,6(4):267-285.
[32]邢淑芬,俞国良,林崇德.小学高年级儿童的内隐智力理论及其与表扬的关系[J].心理发展与教育,2011,27(3).
[34]SENGUL S, KATRANCI Y. Free problem posing cases of prospective mathematics teachers: difficulties and solutions [J]. Procedia-social and behavioral sciences,2015(174):1983-1990.
[35]小学数学四年级上册[M].北京:人民教育出版社,2014:102.
[36]小学数学五年级上册[M].北京:人民教育出版社,2014:113.
[37]CAI J, HWANG S. Generalized and generative thinking in US and Chinese students' mathematical problem solving and problem posing[J]. The journal of mathematical behavior,2002,21(4):401-421.
[38]MUELLER C M, DWECK C S. Praise for intelligence can undermine children's motivation and performance[J].Journal of personality and social psychology,1998,75(1):33-52.
[39]DWECK CS. Mindsets and human nature: promoting change in the Middle East, the schoolyard, the racial divide, and willpower[J]. American psychologist,2012,67(8):614-622.
[41]DWECK C S. Mindset: the new psychology of success[M].New York: Ballantine Books,2007:117-118.
[43]SILBER S, CAI J. Pre-service teachers' free and structured mathematical problem posing[J]. International journal of mathematical education in science and technology,2017,48(2):163-184.
[46]DEGOL J L, WANG M T, ZHANG Y, et al. Do growth mindsets in math benefit females? Identifying pathways between gender, mindset, and motivation[J]. Journal of youth and adolescence,2018,47(5):976-990.
[47][49]BURNETTE J L, OBOYLE E H, VANEPPS E M, et al. Mind-sets matter: a meta-analytic review of implicit theories and self-regulation[J]. Psychological bulletin,2013,139(3):655-701.
[48]OMMUNDSEN Y, HAUGEN R, LUND T. Academic self-concept, implicit theories of ability, and self-regulation
strategies[J]. Scandinavian journal of educational research,2005,49(5):461-474.
[50]DORON J, STEPHAN Y, BOICH J, et al. Coping with examinations: exploring relationships between students' coping strategies, implicit theories of ability, and perceived control[J].British journal of educational psychology,2009,79(3).
[52]李欣莲,宋乃庆,陈婷,蔡金法.小学数学教师“问题提出”表现研究[J].数学教育学报,2019,28(2).
[53]李怀军,张维忠.小学生数学问题提出能力发展研究[J].数学教育学报,2019,28(5).
Research on the Relationship between Thinking Patterns, Academic Achievement and Ability to Propose Questions——Case Study on Primary School Student in Urumqi
DON Lian-chun, YAN Na, SUN Jia
Abstract:This study investigates the relationships among students' mindsets, mathematics achievements and mathematical problem posing abilities. Total number of 333 five-year students from Urumqi City participated in this study. The participants' mindsets, mathematics achievements and mathematical problem posing abilities in three problem posing situations (i.e. free situation, semi-structured situation, and structured situation) were examined and analyzed. The analysis of posed problems were conducted fromtwo aspects: number and quality. The number of posed problems includes four types: the raw number of posed problems, the number of valid problems, the number of problems with different mathematical structure (DMS), and the number of solvable problems. The quality of posed problems involves the originality of posed problems and the flexibility of posed problems. It found that mathematical problem posing abilities of the students scored high in mindsets survey were significantly better than those of the students scored low in mindsets survey. In addition, a significant correlation between mathematics achievements and mathematical problem posing abilities was found for the students scored low in mindsets survey. However, there is no such correlation for the students scored high in mindsets survey. Lastly, the relationships among mindsets, mathematics achievements and problem posing abilities vary in different problem posing situations.
Key words: ethnic minority areas; mathematics education; mindsets; growth mindset; academic achievement; problem posing
责任编辑:彭洪莉
